J’ai toujours trouvé que la résolution de problèmes était une compétence difficile à enseigner. C’est en effet une tâche complexe pour laquelle les élèves doivent utiliser plusieurs compétences : lecture, compréhension, représentation, abstraction, numération, calcul…

J’ai déjà évoqué ici une approche que je mets en place en classe depuis plusieurs années, inspirée de la typologie de Vergnaud, et consistant à bâtir pour chaque type de problèmes un « schéma type ». Cette approche se heurte tout de même pour certains élèves à des problèmes de représentation, tout en proposant un outil intéressant : la boite noire.

Dans ma classe, les boites sont rouges… mais j’ai pu affiner petit à petit leur utilisation. Concrètement, ce sont de simples boites à chaussures percées associées à des cubes de couleurs. En début d’année, lorsque j’introduis le calcul mental, j’utilise longuement ces boites pour additionner, soustraire, trouver le complément. Je montre ce que je fais, je demande aux élèves de trouver ce qu’il y a dans le secret de ma boite, ou ce que j’ai ajouté… et on vérifie en comptant les cubes. Je peux laisser à disposition d’un élève en difficulté une boite et des cubes si ça l’aide. Cette boite est donc dès le début associée au calcul.

Lorsque nous travaillons sur les problèmes, nous commençons par mimer les situations, ou utiliser des représentations réalistes des données du problème. Par exemple, je travaille beaucoup au début sur les problèmes du Petit Poucet qui ramasse ou qui perd des cailloux, et nous comptons les cailloux.

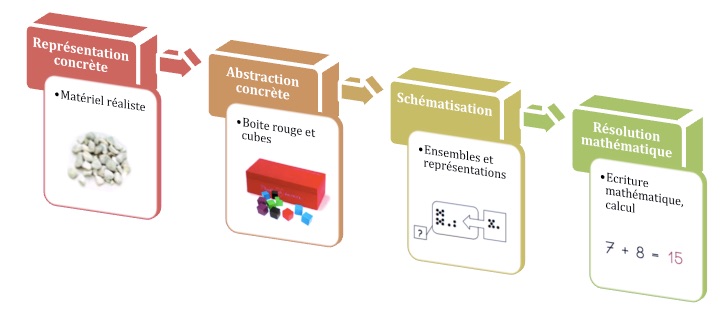
Ensuite, notre boite sert de première marche vers l’abstraction, pour les élèves qui n’arrivent pas à passer directement à une représentation schématique ou mathématique : chaque problème doit pouvoir se vivre avec la boite et les cubes. Pour cela, l’élève doit trouver ce que représentent les cubes, la boite, ce qu’il cherche… Par exemple dans le problème : Maman avait 15 roses, mais elle a retiré les 6 fleurs fanées… Combien en reste-t-il dans son bouquet ? , l’élève doit trouver que les cubes représentent les roses et la boite le bouquet… Utilisée ainsi, la boite est un outil efficace vers la représentation abstraite de la situation. Tous les problèmes portant sur les cardinaux peuvent passer par la boite (pour les problèmes sur des nombres ordinaux, il faudra une bande numérique). Comme notre boite est dans la classe associée au calcul, c’est aussi un passage vers la représentation mathématique de la situation. Bref, c’est une étape importante de l’échelle de progression des stratégies en résolution de problèmes que l’on peut définir avec les élèves comme suit :

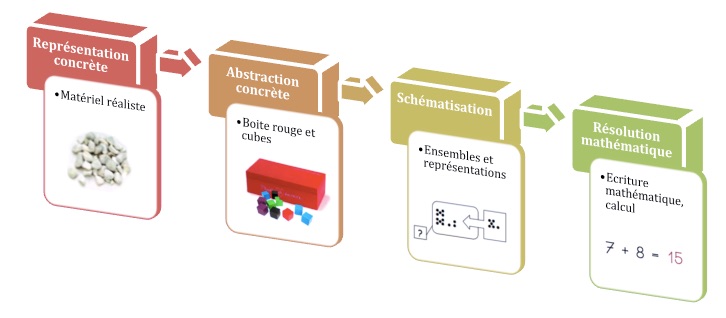
J’ai nommé la phase de la boite, un peu à la manière d’un oxymore, la phase d’abstraction concrète… juste pour se souvenir que la première phase de représentation de la réalité de manière conceptuelle peut rester concrète au niveau du matériel, et que l’abstraction de la pensée ne signifie pas forcément l’absence de manipulation.

Il est important que les élèves sachent que la procédure experte, celle vers laquelle ils doivent progresser, est la procédure mathématique. Mais ils doivent pouvoir revenir vers d’autres procédures si besoin, quand ils découvrent un nouveau type de problème, quand ils ne possèdent pas encore les concepts mathématiques (situations de partage…), ou quand ils ne parviennent pas à se représenter un type déjà rencontré. S’ils n’arrivent pas à schématiser, alors, ils peuvent utiliser la boite.

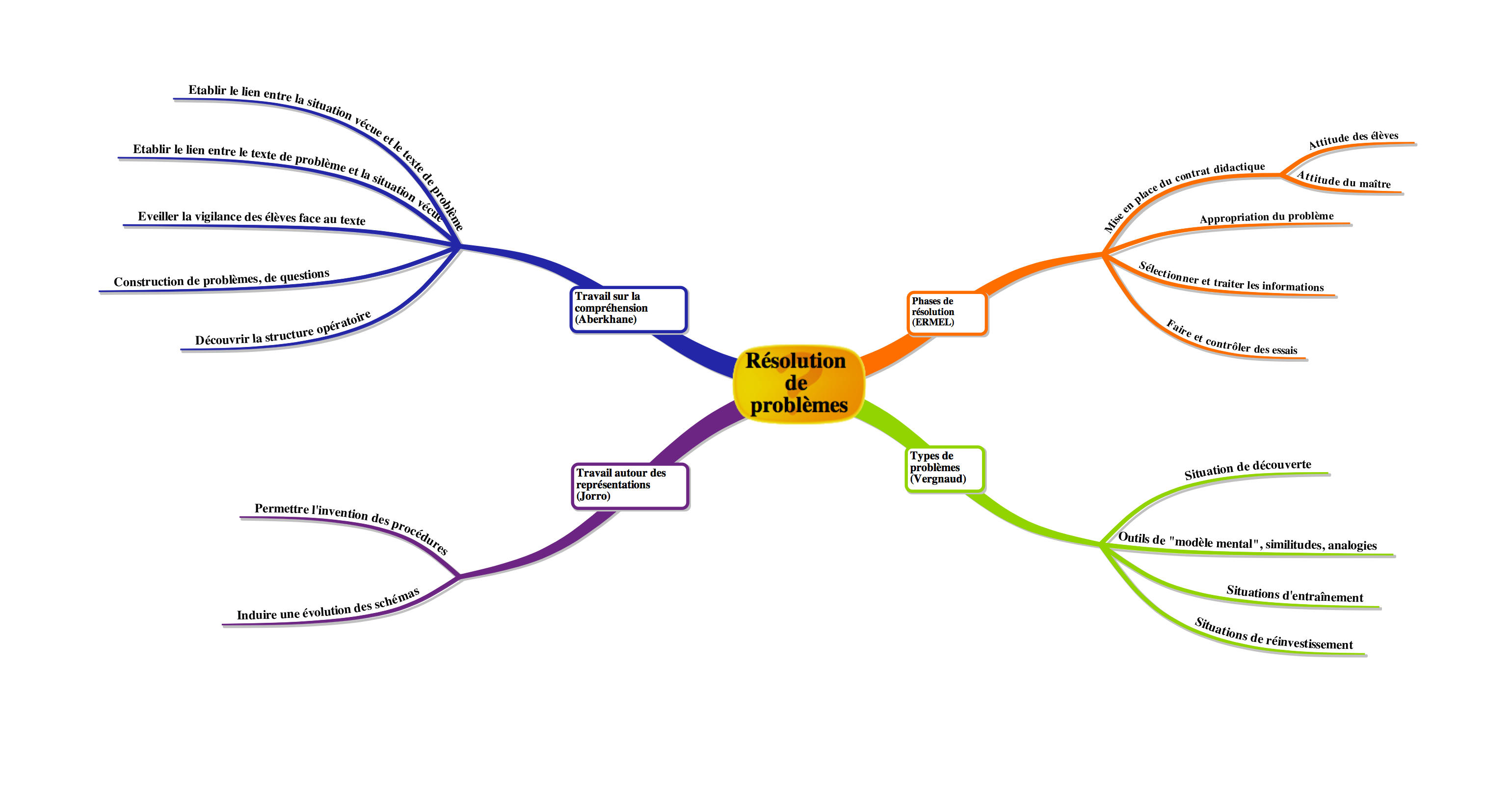
Ce travail progressif permet de mettre en oeuvre plusieurs dimensions de la résolution de problèmes, soulevées par différents didacticiens :

• le travail sur la compréhension, le lien avec le vécu, la vigilance face au texte, dont parle Aberkhane ;
• le travail autour des représentations et de leur évolution, décrit par Jorro ;
• le travail sur l’appropriation du problème et la sélection des informations, mis en avant par le groupe Ermel ;
• le travail autour de la modélisation des types de problèmes, structuré par Vergnaud.

Il faut associer à ce travail une explicitation de la démarche méthodologique, afin d’outiller au mieux les élèves, comme par exemple :

Pour résoudre un problème, je dois : 

• lire l’énoncé et le comprendre (le relire si besoin)
• me représenter la situation dans la tête, ou avec l’aide d’un schéma ou de la boite
• chercher l’écriture mathématique
• chercher la solution, à l’aide d’un schéma ou d’un calcul
• vérifier que la solution est possible
• écrire une phrase de réponse à la question.

Comme souvent dans ma classe, cette structuration a fait l’objet de la construction collective d’une affiche et d’un aide-mémoire individuel :

Si vous voulez retrouver le contenu de cet article en format pdf, le voici :

Et pour les phases d’entrainements, encore des boites sur le blog : les boites à problèmes…